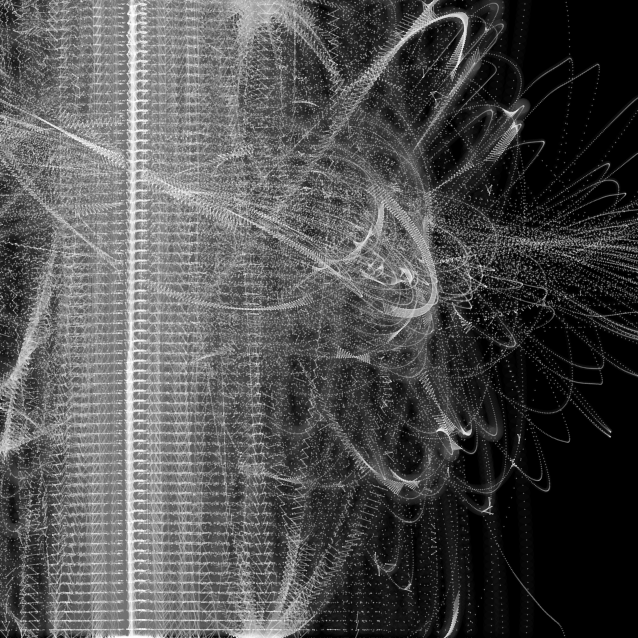
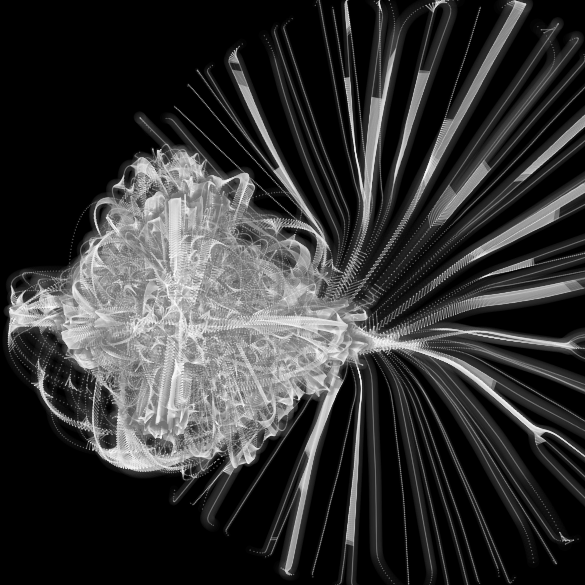
Algorithmic Art

by: Waqasul Haq

Introduction

Algorthmic Art is a collection of generative art works, in which I explore the creation of patterns, geometric forms and emergence. They embody motion and smooth oscillatory transformations on the screen, exploring combinations of tools and techniques to create geometric stuctures. These artworks are in someway, partly or wholy automated by computational decisions and algorithmic decisions. This can often result to having unxpected outcomes, which creates new alien beauty to explore as an artist.

Prior Inspiration

Before creating any sort of algorthmic artwork there needs to be a source of inspiration, the inital ideas to create generative art came from the artist John Whitney [2] who from the 1960s onwards, started to produce artwork that intends on using the computer to animate and render the graphics. Whitney's work combines the smallest rules of geometry and motion in order to create these beautiful flower-like patterns.

John Whitney - Catalog

Tools of Creation

The idea was then, not to focus mainly on creating aesthetically pleasing images but to learn and understand the mechanisms by which we can make tools for generative art. This way, learning the concepts behind the generative art and how it is made, allows in the future, for a deeper exploration because we can reference back to the techniques used to create the artworks. Also because code can be seperated into objects and functions, it allows one to create objects and utilities that encapsulate a tool's functionality within it. I have gone on to make several objects and utilities that allow me to easy create artworks by simply initialising the objects

Parametrics

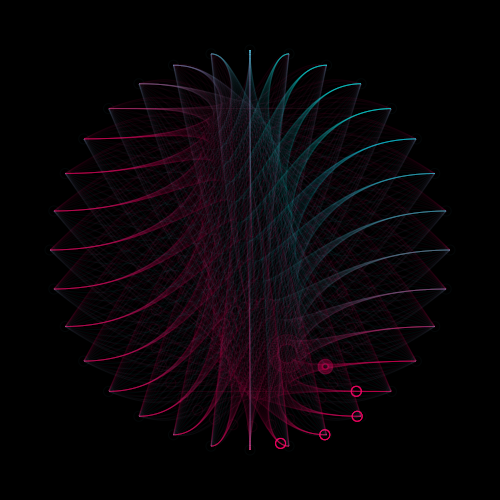
The first set of tools that I decided to develop and use to produce computational artworks are parametric equations [4]. A parametric equation is where an equation is taken and broken down into its respective counter-parts. For example, take a polynomial equation (curve), which can be represented by y = ax^2 + bx + c  is rewritten as two seperate equations y = at^2 and x = t.  A third variable t is introduced to keep track of time. Both of these equations were written as seperate functions, for example:

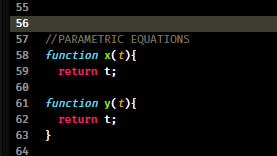
The idea is to then treat these functions as if they are number generators, whereby you pass in a number and you get a number back, the actual value of this number is dependent on what the variable t is - at point point in time we are. To create a Whitney like animation, the method was to create a set of parametric equations for each position vector that we want on screen.

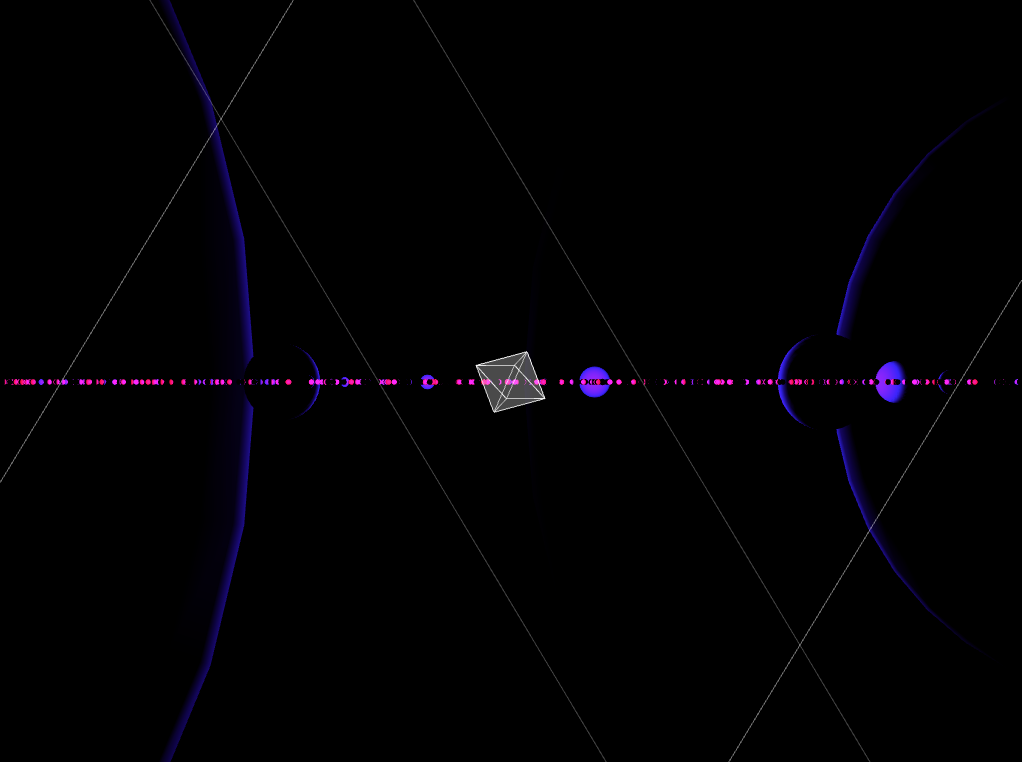
To learn how to achieve the Whitney like patterns (from this video here) [1] it was evident that if you create a more than one set of equations and then draw a line between them, when we vary the parameters of the numbers that are generated we get really interesting patterns. The most useful number generator are the trigononmetric functions, which return oscillatory values and when stacked (via multiplicative and additive synthesis) creates an evolving piece.  I was able to apply the technique in order to create the following animation.

As an extension on that, there had to be a way to explore all of the different visuals that these equations can produce. Playing about with these equations over-time hinted that a slight change in values can drastically change the way the visuals came out. To solve this issue, I used a minimal user-interface, implemented by the p5.dom.js library. I was able to put sliders and their subsequent values to create this interactive piece. Which allows you to explore the different values. You can access this here.

Artworks using this tool.

Parameterics can also be used to create oribital motion, which can then be used to create solar systems, so as a side project I created this solar system here, the data for the planets are kept as a seperate array of objects, this way the values are passed into the planet-render function. Access here.

Bezier Functions

I also wished to experiment with bezier curves, as they are useful to create smooth motion graphics and useful for path following. The functions that are already available with p5 don't have a bezier-path function, instead the function draws the bezier curve between two given points. I wanted to only calculate the next point off the bezier curve, depending on the time.

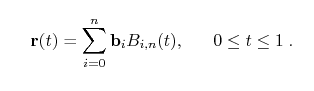
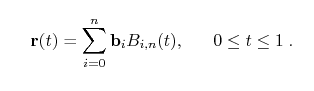
Though at first there was a learning curve and I was struggling because the Bezier Function requires you to know the basics of Mathematical summation and series relation. After doing some mathematical practice with sequences and series and understanding how the summation notation works, I was able to create a Bezier Curve formula that computes the next point in space, based on a time value between 0 and 1. 

Bezier Curves have control points and using this functions theoretically one could produce a function that allows you to render a bezier path with any amount of control points that you wish to have. 

To create a generative piece, I drew the curves in a circle and connected every point to every other point using a bezier curve, after which I then used my bezier animation function to draw ellipses moving across those bezier curves, I knew my function worked because the shapes follow the path regardless of the fact that we are actually rendering the curve.

Here are some artworks produced from that (you can acess the sketches here):

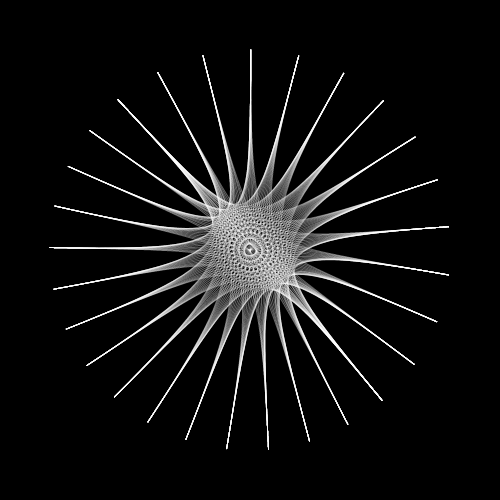
Lissajous

The next tool sticks closely to the instrumentality of the previous one, where still we have a set of equations but this time it is the famous lissajous equations, these I found to be really beautiful in their symmetry and from simply adpating the technique we learned before with parametric equations we can create formula with parameters that can be changed and to see what results. [5].

The smooth looping nature of the lissajous movement inspired me to further apply this tool to motion, the collection of particles moving on lissajous lines with different parameters gives the impression of a swarm of insects. You can find that here.

Sometimes small changed in rules can change a whole picture, I took it a step further by creating a function that draws lines between every single particle on screen, I added some optional user interaction whereby the user can erase the background and see the trails that have been left behind, you can access it here. Use Space to erase/draw the background, R to reset/change colour, T to rotate, Y to switch direction and U to oscillation in size.

To create further exciting results I wanted to see what the lissajous system renders if there were to be numerous particles on screen, each with its own randomised lissajous path, this produced some of most striking results, aesthetically, it reminds me of a tendrils that are coming off of a magnetic field or a starcluster in a galaxy, where you can see the stars swirling, using the same controls as above I can erase and unerase the background - find it here.

Parametric Engine -

Condensing the parametric equations into an object where you can have an array of n-control points and assign what you wish to return - theses can be used to create art - here is an example I have done in WEB_GL mode in p5.js.

Geometry

After exploring curves and motion, it was time to start looking into form and how geometry works computationally. At first I struggled with the idea of creating a simple geometric shape from scratch, the only way to create an n-side polygon or an n-sided star was to hard-code it, however this means that the function is no long modular and cannot be reused (supposing we wanted to resize and draw it at different places). The solution for this was much simpler than tought, there is no need to hard code any polygons because polygons are essentially lower-resolution cirlcles, this meant that I can create a circle using polar-coordinates, then determine the increment of the angle to the number of sides that we want. 

Say we wanted 5 sides to a polygon, a full turn of a circle is 2pi or 360 degrees, so to determine how many degrees or radians we must turn by to produce the shape, we have to divide the period of the trigonmetric function we are using by the number of sides, for example a pentagon would be 5 sides, so 360/5 = 72. I used the beginShape() and endShape() built in functions in p5, which allowed me to create fully formattable functions. Here is an interactive example of that function, the mouseX value is mapped to the polygon resolution, access here. 

I developed these functions as an addon for the p5.js library, adding in a new polygon function and a start function (both also have an optional contour, which draws the cut-out version of the parent polygon from the middle of the shape). Declaring the function as part of the p5.prototype object, so now when you add it as an extension, there are four functions to use: basicPolygon, basicContour, starPolygon, starContour. These can be called like normal p5 shape functions except they are more customisable. You can access the geometric part of my artworks on this page.

Artworks:

Attractors And Emergence

For the final set of generative images, I wanted to look into emergence and the building of complex generative shapes that arise out of a simple set of rules. I found that symettry looks attractive and beautiful but now it was time to explore what would happen if you broke that symmetry, to create random chances and possible outcomes. By breaking symmetry I allowed myself to focus more on the chaotic properties that computing art can bring about, unexpected changed and fluctuations, all due to the stacking of simple rules.

Inspired by Casey Raes

While deeper into generative art, I ran into the artwork of Casey Raes, who produces a system or a tool, which is comprised of a simple set of rules. These simple rules turn out to be powerful because when we get to a larger scale,  these simple rules start to create complexity, this was facisnating. It started to break down ideas I had about computational art being geometrically perfect and now allowed me to start exploring and creating things no one has seen before. 

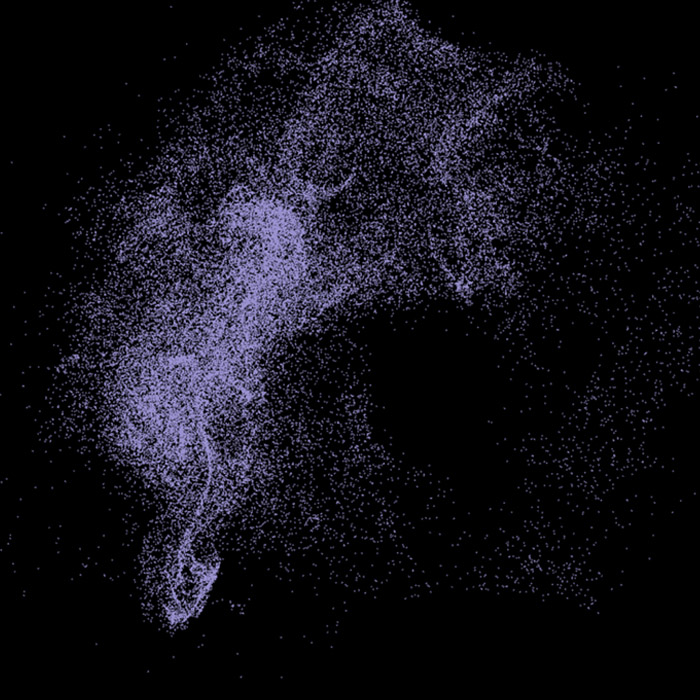
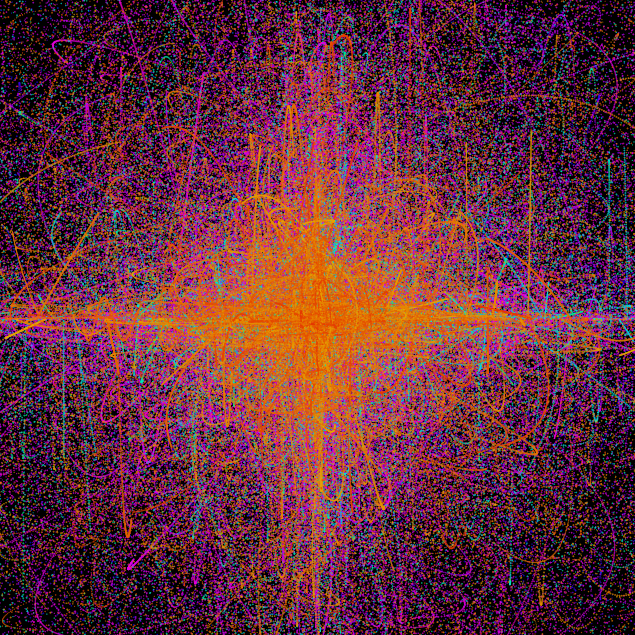
The general technique behind these I discovered was that the screen is full of dumb agents, moving randomly outwards in all directions. The simplest rule is introduced to the simulation and it produces amazing and emergent results. The rule used here is to just draw a line between two objects when they intersect. Once the opacity for the lines is turned down and the background is not refreshed, we get amazing like tendrils and natural forms, they appear to wisp in and out when they intersect. 

Also depending on where you start the agents, it produces a different pattern, here are some examples of artworks I have done, as you can see the particles have been started at different places, along a circle, inside a square, even following lissajous paths. These are then set free to draw.

Here is my attempt:

Stepping it up

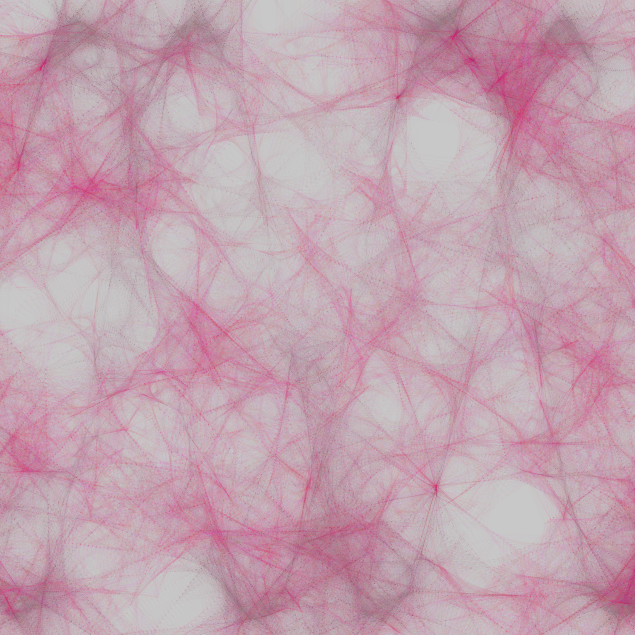
To further add rules to this equation, I went on to study gravitational attractors and steering behaviours. I wanted to advance from the standard dumb agents on screen. I wanted to have the same set of rules on-screen as before, with the intersection causing a line to appear. 

This time however I have looked deeper into vectors, forces and steering behaviours from The Nature of Code by Daniel Shiffman. I took from it, some basic flocking behaviours - as I did not want code too complex for a general drawing program. By adding flocking behaviours, the agents knew the others' locations on screen and steered themselves around the canvas accordinly. This is then paired with random attractors, which then cause even more complex patterns to emerge. 

I personally felt that creating the emergent art, from the simple set of rules was much more rewarding than following the standard geometrically symetrical artworks, it produced almost creaturely patterns, here is the final set of artworks.

Sources

[1] https://www.youtube.com/watch?v=LaarVR1AOvs | Recreating Vintage Computer Art

[2] http://www.awn.com/mag/issue2.5/2.5pages/2.5moritzwhitney.html | John Whitney Bio

[3] http://tutorial.math.lamar.edu/Classes/CalcII/ParametricEqn.aspx | Parametric Equations

[4] http://web.mit.edu/hyperbook/Patrikalakis-Maekawa-Cho/node12.html | Bezier Curve

[5] http://mathworld.wolfram.com/LissajousCurve.html | Lissajous

[6] https://www.youtube.com/watch?v=_8DMEHxOLQE | Casey Reas Draw With Code

[7] http://natureofcode.com/ | Nature of Code