Published in: O.E. Barndorff-Nielsen and E.B.V.
Jensen (eds.),
Geometry in Present Day Science,
World Scientific, Singapore, (March 1999), pp. 187-208.
Abstract
Delaunay graph, which connects all minima and saddle points. This graph devides the plane into regions. In each of
the compact regions, there is exactly one maximum, the non compact regions don't contain a local maximum.
At the end we classify all those graphs if P contains of 3 or 4 points.
Summary
NB: Use of some terms is from FFL (e.g., generators).Introduction
One can study either the distance, d(X)=min{d_i(X)}, from point generators, Pi, or the distance squared functions, D(X)=min{d_i^2(X)}: they share similar level curves, maxima, minima and saddles. D however gives nicer formula for the gradient (and differentiability at the generator loci).The restriction of D to the interior of Voronoi cells is differentiable, and the loci where D is not differentiable is precisely the Voronoi Diagram (VD(P)).
Level curves of d can be considered as wavefronts, {d = u}, which bounds sets {d x u}, and which start from the generators P. It is the change of topology of these sets {d x u} which is studied here.
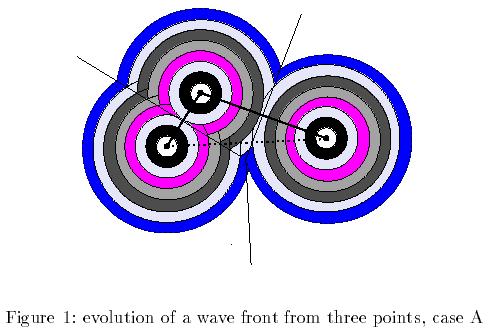
Consider, as a 1st example, three point generators (in a general configuration; e.g., not co-linear) in the plane:
- Initially, each generator is surrounded by a circular wavefront, and hence, the Euler characteristic is Euler = 3.
- Next two wavefronts meet at a point and we get 2 contractible sets; hence Euler = 2.
- Later the 3rd wavefront meets the newly formed (combined) set and we get only one resulting set, hence Euler = 1.
- For case A (obtuse triangular configuration of
generators), the final region gets larger and larger, and Euler = 1 throughout (Figure 1).
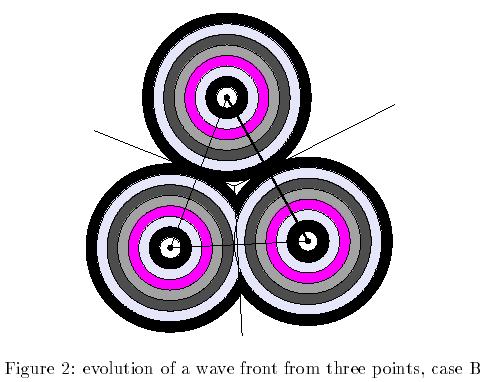
- For case B (acute triangular configuration of generators), all angles are sharp, and the wavefronts meet one more time enclosing a region in the middle. The set {d x u} is "circular" and no longer contractible, such that Euler = 0 (Figure 2). As the wavefronts keep propagating, the enclosed region vanishes, and Euler = 1, there is only one set left, which is contractible, and there are no more topological changes if u keeps increasing.
NB: One need more refined information than just the Voronoi Diagram to understand the topology dynamics of wavefronts.
Behaviour of D on the plane A^2

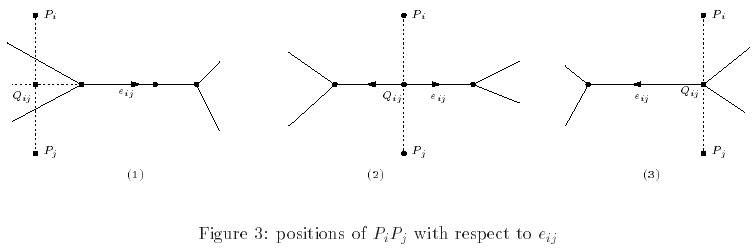
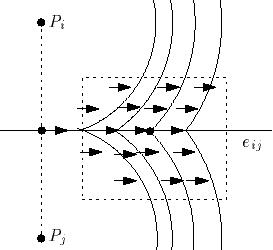
Consider a point A on the interior of a Voronoi edge eij:
- If A is different from
the center of the line PiPj
(midpoint Qij between the
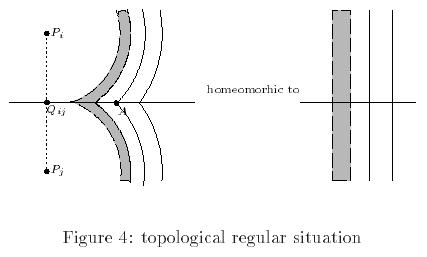
pair of generators), then there is no change in the topology of the
lower level sets {d x u} since
the level curves of D are
homeomorphic to parallel lines, and thus A is a topological regular point of D (Figure 4).
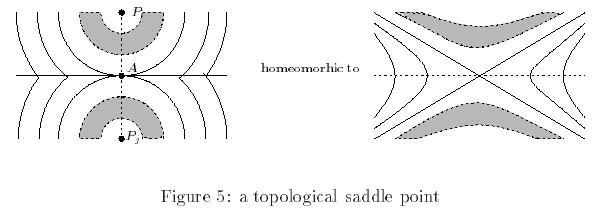
- If A coincides with Qij,
then the local map corresponds to a differentiable saddle point, and A is called the topological saddle point of D (Figure 5).
We are now left with A being a vertex of the Voronoi diagram:
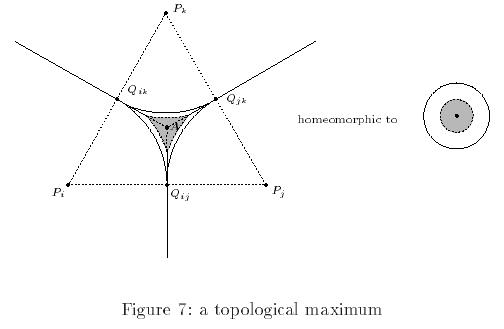
- If A is a maximum of
each edge intersecting at the vertex locus, then A is in fact also a local maximum
of D (Figure 7) ---
necessarilly an interior (circumcenter) point to the triangle with
three generators as vertices.
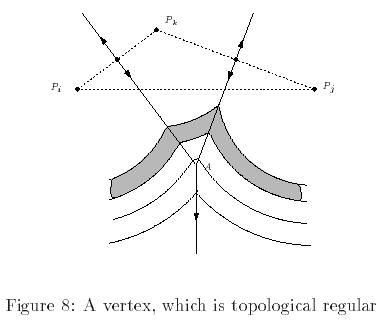
- If A is a maximum on all but one of the adjacent edges, then, locally, D is equivalent to a linear function and A is again a topological regular point of D (Figure 8) --- necessarilly an exterior (circumcenter) point to the triangle with three generators as vertices.
- There is no other (possible) case to consider.
Main Theorem
- Theorem: Let m, s, M be the number of topological minima, saddle points and maxima of the distance function D, then:
- Definition (index of critical pts.): m, s, M are called critical points of index 0, 1, 2. with corresponding (distance) value called critical value.
- Definition (regular pts): All other points of D are called (topologically) regular; they come in 3 flavors:
- Differentiable regular points in the interior of Voronoi cells.
- Topological regular points in the interior of certain Voronoi edges.
- Topological regular points which are multiple points.

Proof:
The proof involves defining a vector field which flows continuously everywhere except at the critical points. A natural candidate is to use the gradient of D. Special care is only needed near the Voronoi diagram where D is not differentiable.
- Build a vector field on the interior of Voronoi cells by considering the gradient direction of a differentiable function f (= D):
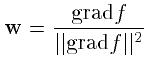
- Near Voronoi edges eij
but away from saddles and Voronoi vertices (multiple pts), define w to be parallel to an edge eij (Figure 12).
- Near multiple pts (Voronoi vertices) which are regular, define w
to be parallel to the outgoing Voronoi edge (Figure 13).
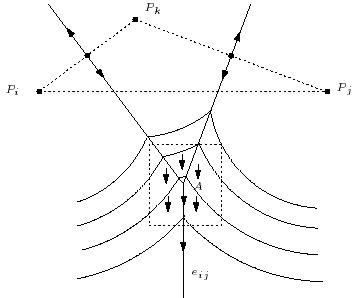
Figure 13. Near a Voronoi vertex which is topologically regular.
- Near each generator, local minimum of D, the topology is that of a disk for a small enough distance encircling a 0-cell.
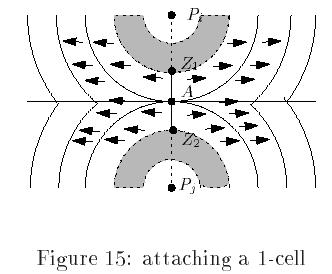
- In a small neighborhood near a saddle point, A, a 1-cell (interval Z1Z2) gets attached (Figure 15).
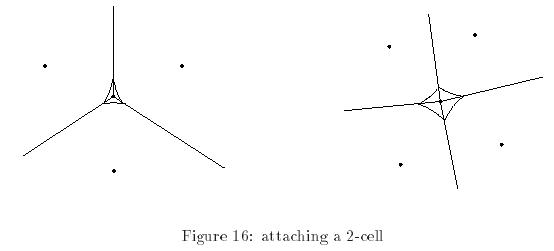
- In a small neighborhood surrounding a local maxima, A, a 2-cell (filled disc) gets attached
(Figure 16).
Graphs
The Delaunay graph related to the set of points P
The vertices of the Delaunay graph are the generators themselves. The graph contain an edge connecting a pair of generators iff their Voronoi cells share an edge.The sm-graph related to the set of points P
The vertices of the sm-graph are the generators themselves, local minima of D. The edges are those line segments PiPj which intersect a Voronoi edge eij in its interior, which are 1-to-1 correspondance with the saddles, s, of D, via the intersection (mid-)points Qij. This graph is called the saddle-minima-graph of P or sm(P) for short; it coincides with the Gabriel graph of P.- sm(P) is a sub-graph of
the Delaunay graph.
- sm(P) is connected.
- sm(p) coincides with the
Gabriel graph of P (or is included in it if right triangular
configuration are considered or not as part of the Gabriel set).
- Proposition: The number of bounded regions defined by sm(P) is equal to M, the number of maxima of D, such that for each region there is exactly one maximum in its interior.
Enriched Voronoi Diagram
The Voronoi Diagram can be considered as a planar graph with extra infinite edges --- but one can compactify this situation by adding one (virtual) generator at "infinity" and get in that way a graph on the sphere. By adding as nodes of the graph the saddle points, one can also add arrows to the graph in the directions of increasing distance values. The resulting directed graph, the "enriched Voronoi Diagram," contains all the topological information studied here (Figure 20).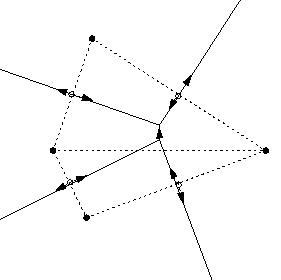
Figure 20. The enriched Voronoi Diagram.
Configurations with 3 or 4 generators
The Delaunay edges which are not included in sm(P) are dashed in Figure 21.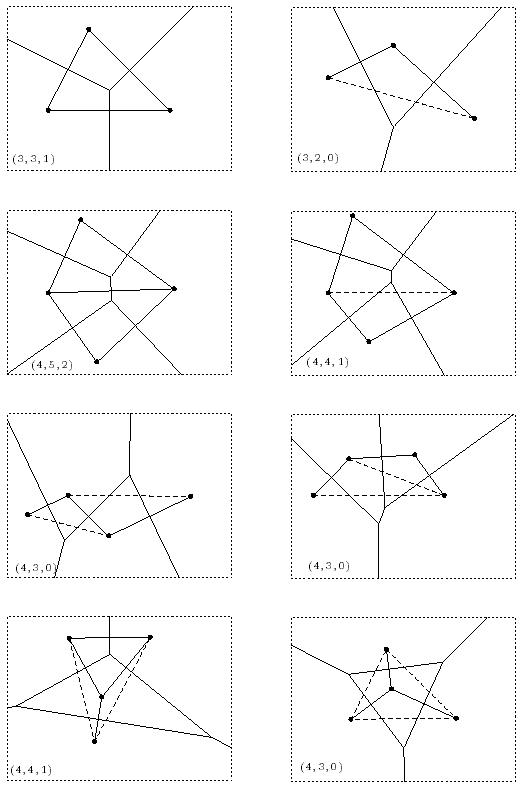
Figure 21. Generic configurations with 3 or 4 generators.
The notation is defined as (m, s, M).