Last update, Dec.10, 1998
Publications on Projective Geometry :
Publications on Perspective Geometry :
BibTeX references .
by Jim Blinn
(MSR - Graphics)
IEEE Computer Graphics &
Applications, v.18(6), Nov/Dec. 1998, pp.78-80, Jim Blinn's Corner.
Explains the concept of cross ratio in projective geometry and proves it (easy explanation).

par Roger Laurent, Cedic/Nathan: Paris, 1987, 316 pages.
Problème: étant donné une perspective, où en général ne figure pas la position de l'observateur par rapport au tableau, retrouver les dimensions géométrales du dessin ainsi représenté, à une échelle donnée. (Peut-on aussi reconstruire un bâtiment ainsi?)
La résolution de ce problème pré-suppose que le tableau soit perpendiculaire au plan géométral et que l'on puisse déduire les 4 données suivantes (qui caractérisent une perspective):
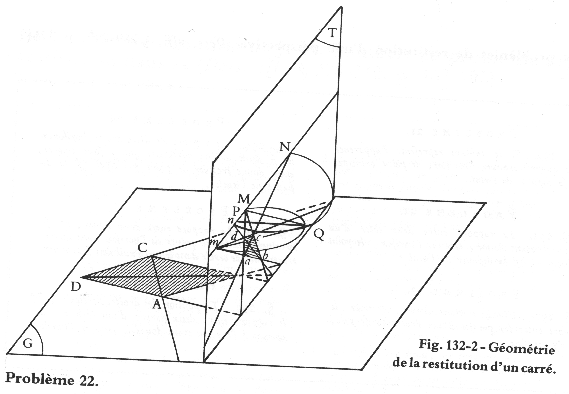
"Find the Horizon Line, the Eye Station and the Principal Distance, from the 2PtP of a square."
Let abcd be the perspective image of the square ABCD in Ground Plane G. The parallel sides of the square, ab & cd define the VP m, while the parallels ad & bc define the VP M. These 2 VPs thus define the Horizon Line (HL).
Furthermore, mbM must be a right angle (in space). The same is true of the diagonals acN and bdn. Hence, the VPs m & M and the diagonal intercepts with the HL, n and N, determine two circles upon which the Eye Station Q must lie. This determines Q as the intercept of both (half-)circles. N.B.: These 2 half-circles are called "arcs capables d'angles droits" in French.
Finally, the orthogonal line from the Eye Station, Q, to the Horizon Line determines the Pincipal Point , P. The (scaled) length QP is then the Principal Distance, f (or focal distance).

Square in 2PtP: finding the eye (Q) & PP (P).
Resolving the square in 2PtP.
"Find the Horizon Line, the Eye Station and the Principal Distance, from the 2PtP of a rectangle, knowing the ratio of its two sides."
Assume the ratio AD/AB is known for the rectangle ABCD. Then, the internal angle alpha = DBA is also known (since DAB is a right angle): alpha = arctg(AD/AB). This is also the angle associated to dab, the perspective projection of DAB.
Consider now the VPs m & n associated to the directions BA & BD (or ba & bd in perspective), respectively. These 2 VPs determine the Horizon Line, as usual.
Furthermore, Q, the Eye Station, must be on the half-circle through m and M as usual, where M is the VP for the other side of the rectangle. i.e., BC (bc).
Then, alpha = mQn, since Qm is parallel to BA (ba) and Qn is parallel to BD (bd). Thus, we have the following geometrical construction to retrieve the locus of Q on the "cercle capable":
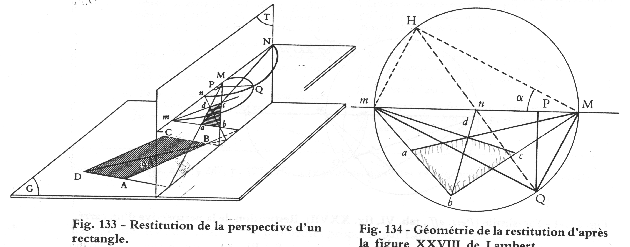
Resolving the rectangle in 2PtP.
by Kirsti Andersen,
In "Sources in the History of Mathematics and Physical Sciences", vol.10, Springer-Verlag, 1992.
Introduces a particular form of "cross-ratios", where one of the four points is a vanishing point (p.28).
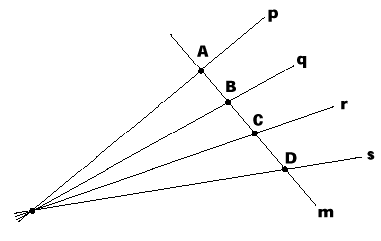
Uses an angle-scale on a vanishing line and the semi-circle including the eye to find how to draw 2D figures making an angle with respect to the viewer (pp.30-33).
Considers certain Inverse problems of perspective.
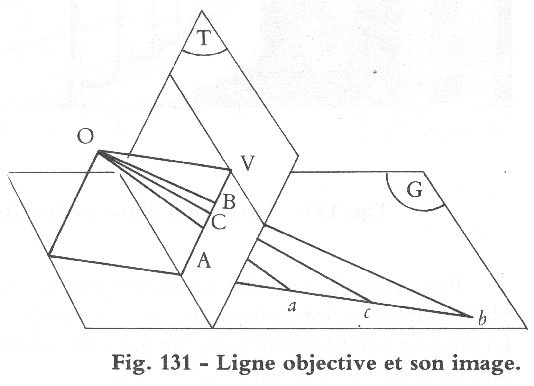
 |
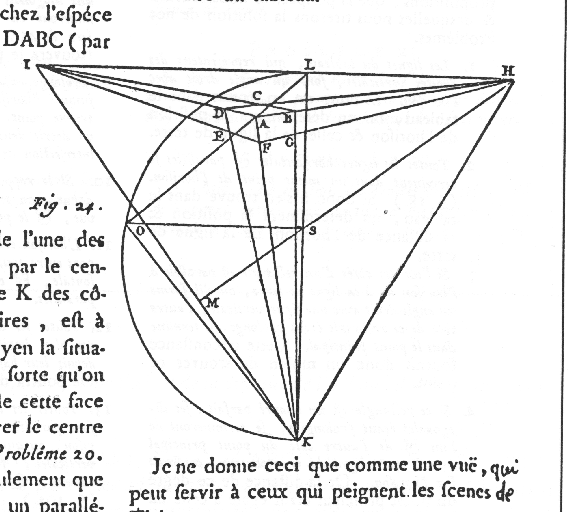 |
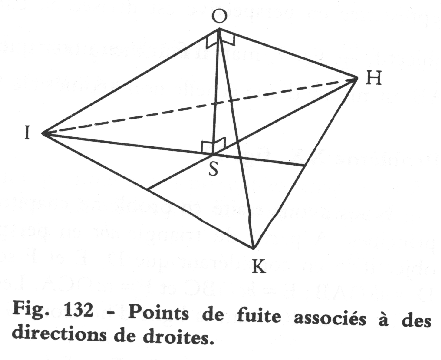
| VPs IKH & Station Point (O) generate the visual tetrahedron. S is the ortho. projection of O & orthocenter of triangle IKH . |
Resolving the visual tetrahedron, given a cube in 3PtP. |
Mention of John Hamilton's "Stereography or a Compleat body of Perspective" (London: 1738, 1749), where the curve of foreshortening is studied (an hyperbola):
Page created & maintained by Frederic Leymarie,
1998-2001
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu