BibTeX references.
Link at Beckman Institute.
Link to Aizu's team other related publications.
Masaki Hilaga, Yoshihisa Shinagawa, Taku Komura and Tosiyasu L. Kunii
Proceedings of SIGGRAPH
2001, Computer Graphics Proceedings, Annual Conference Series,
pp.203-212 (August 2001). ACM Press / ACM SIGGRAPH. Edited by Eugene
Fiume.

There is a growing need to be able to accurately and efficiently search visual data sets, and in particular, 3D shape data sets. This paper proposes a novel technique, called Topology Matching, in which similarity between polyhedral models is quickly, accurately, and automatically calculated by comparing Multiresolutional Reeb Graphs (MRGs). The MRG thus operates well as a search key for 3D shape data sets. In particular, the MRG represents the skeletal and topological structure of a 3D shape at various levels of resolution. The MRG is constructed using a continuous function on the 3D shape, which may preferably be a function of geodesic distance because this function is invariant to translation and rotation and is also robust against changes in connectivities caused by a mesh simplification or subdivision. The similarity calculation between 3D shapes is processed using a coarse-to-fine strategy while preserving the consistency of the graph structures, which results in establishing a correspondence between the parts of objects. The similarity calculation is fast and efficient because it is not necessary to determine the particular pose of a 3D shape, such as a rotation, in advance. Topology Matching is particularly useful for interactively searching for a 3D object because the results of the search fit human intuition well.
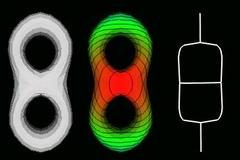
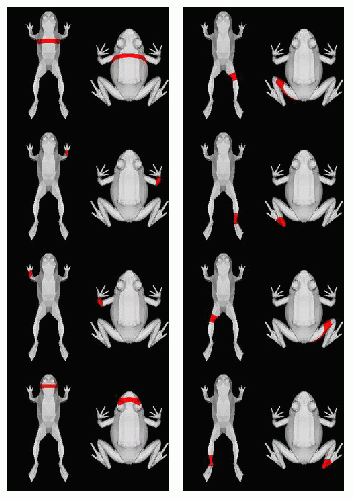
Not good enough: Reeb graph changes with orientation.
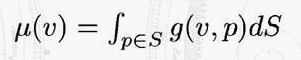
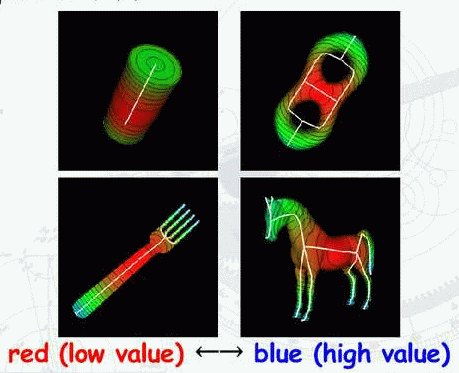
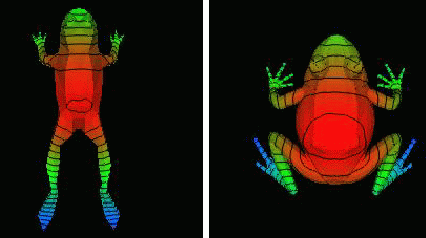
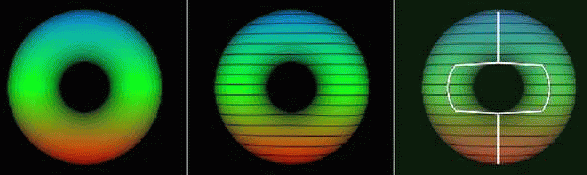
Deformed frog and distribution of function mu (relatively
stable).
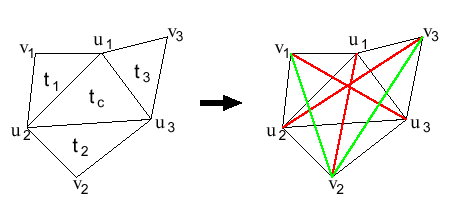

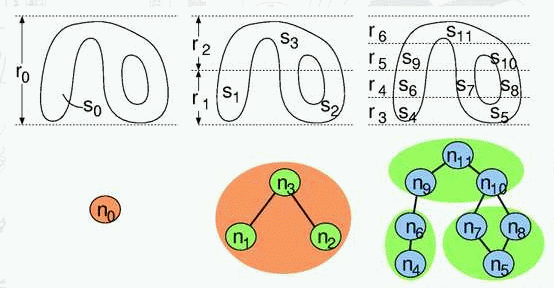
Example of bases and area of bases.
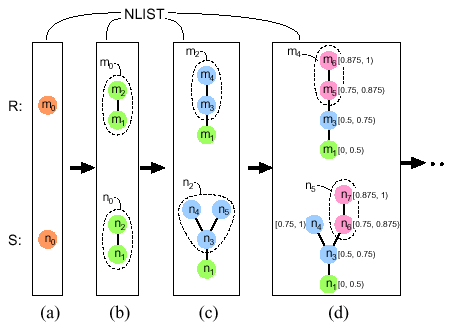
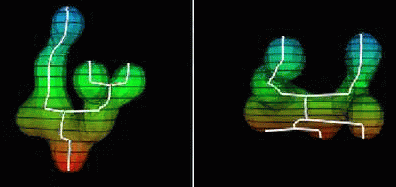
Overview of the matching algorithm.
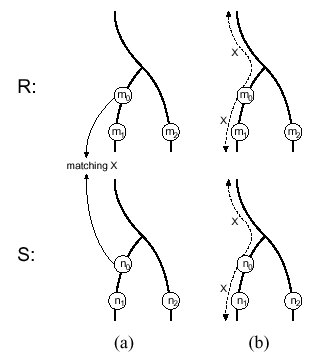
Propagation of matching label.
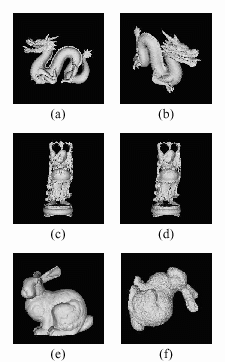
(a) dragon and (b) rotated, scaled, translated dragon
(c) Buddha and (d) simplified Buddha
(e) bunny and (f) simplified, noisy, rotated, scaled, translated bunny
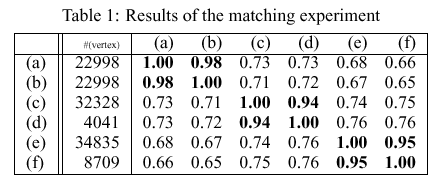
Similarity numbers >= 0.94 for appropriate pairs (e.g. (c) and (d))
Range [0.65, 0.76] for wrong pairs (e.g. (d) and (f))

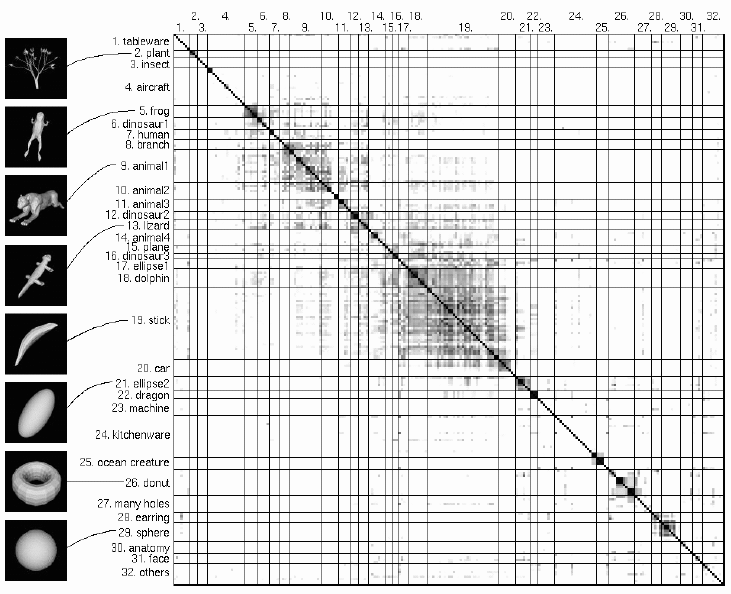
Similarity matrix for all 230 models, divided into 32 categories.
Darker square = higher similarity.
Similarity < 0.75: clamped to white (i.e. to similarity of 0).
Chiew-Lan Tai, Yoshihisa Shinagawa and Tosiyasu L. Kunii
Computers & Graphics
Volume 22, Issues 2-3 , 6 March 1998, Pages 255-268
The shape data of many complex objects, such as anatomical structures, are available in the form of contour slices. To visualize these complex shapes, most existing methods focus on resolving the contours connectivities and generating surface models. These methods do not offer any way of abstracting characteristic features from these complex shapes. To address this problem, Morse theory has previously been proposed as a topological abstraction tool, and a Morse theory-based surface coding system has been developed to code complex shapes as a sequence of basic operators. The topological structure of the coded surface is, however, implicitly stored in the operators. Topological information is thus not readily available without evaluating the operators. This paper proposes a more versatile representation by incorporating a contour containment relation into the earlier representation. With the explicit topological information, non-sequential construction and modifications can be performed without violating topological integrity. Editing operators similar to the Euler operators are also proposed.
Author Keywords: critical points; contours; Reeb graph; topology; Euler operators
Yoshihisa Shinagawa, Tosiyasu L. Kunii, Alexander G.
Belyaev and Taketo Tsukioka
The International
Journal of Shape Modeling, 2(1):85-102, March 1996.
To analyze given object shapes, it is necessary first to model the shapes and then to analyze the models. This paper proposes a method of modeling and analyzing two-dimensional (2D) and three-dimensional (3D) shapes based on singularities. First, a function is defined on an object. The object is then modeled by the distribution of the singularities of the function. Finally, the extracted singular points are analyzed by a Reeb graph together with wavelets for multiresolution analysis. The applications of the method include analysis of botanical leaf shapes and human facial expressions.
Keywords :
To understand the essential properties of given data of object shapes, it is necessary to abstract them. The data is often given in the form of mesh data and equi-height contours in the case of terrain shapes, and cross-sectional images in the case of CT or MRI of human organs. To abstract such shape data, we have proposed a method based on singularities.
The basic idea is to define a function on the object and use the singularities of the function to abstract the object shape. First, let us take an example of a function k:x -> k(x) defined on a curve parameterized by x. In this case, the singular points are the maxima, minima and the inflection points of the function k. The singular points represent the global structure of the curve. Let us take another example of a three-dimensional (3D) solid object. In this case, we define a height function $h$ on its surface with its height axis in the z-direction. h gives the height of a point P located at (x,y,z) on the object surface; i.e., h(P) = z. The singular points of the function h are the peaks, passes and the pits of the object surface. We represent the shape of the object by describing the singular points together with the relationships among them. We call the description codes in what follows.
A singular point is said to be nondegenerate if the Hessian matrix H of the function is at its full rank. The number of negative eigen values of H is called the index of the singular point.
The singular points are closely related to the topology of the object, and hence suitable for abstracting its shape In a word, the singular points work in a similar way as the vertices, edges and faces of polyhedra; i.e., they represent the topological skeleton of the object. To be more precise, in the case of a function defined on the 2D surface, a singular point with index 0 is a pit, and it corresponds to a vertex of a polyhedron. A singular point with index 1 is a pass, and it corresponds to an edge. A singular point with index 2 is a peak, and it corresponds to a face.
This paper explains how to use the abstraction method of shapes by singularities for various types of data: bounding curves, equi-height contours, cross-sectional images, surface normals and mesh data. The applications that can be covered are the analysis of botanical leaf shapes, terrain shapes, human organs, and facial expressions.
Shigeo Takahashi, Tetsuya Ikeda, Yoshihisa Shinagawa,
Tosiyasu L. Kunii and Minoru Ueda.
Computer Graphics Forum, 14(3), pp. 181-192, 1995.
(Proc. of Eurographics '95)
We proposed a robust and exact method that extracts the singular points from the discrete elevation data while satisfying the Euler equation, and also a method that converts a surface network to the Reeb graph.
Yoshihisa Shinagawa, Tosiyasu L. Kunii, Hideyuki Sato
and Masumi Ibusuki
Computers &
Graphics, 19(1): 21-28, 1995.
The interference of the motion paths of objects has been an important theme of research. The previous works concentrate on detecting collisions and finding colliding points, and little has been done on characterizing the contact of two objects considering the structures of the space between the objects. This paper proposes a novel method to characterize the interference of objects. Our method is based on the analysis of the structures of the complementary space of 3D objects. The topological structures are analyzed using the coding method based on the Morse theory and the Reeb graph. The method is applied to actual dental articulations to validate the model.
Yoshihisa Shinagawa, Tosiyasu L. Kunii, Anatoly T. Fomenko and Shigeo Takahashi
In: Larry Rosenblum et al., editors,
Scientific Visualization: Advances and Challenges
(Proc. Workshop on Visualization), pp. 309-322, Academic Press, 1994.
This paper proposes a new method to code the surface of a three-dimensional object using mathematical primitives called atoms. This method is an expansion of the method that codes the smooth surface of a natural object such as a human organ by the singular points of the height function based on Morse theory. It allows to handle the cases where there is more than one singular point on a level cross-sectional plane. Using the atoms, non-orientable surfaces such as the two-dimensional projective space and the Klein bottle can be coded. The method is further expanded to allow direct description with multiple height functions.
Yoshihisa Shinagawa and Tosiyasu L. Kunii and Yannick
L. Kergosien
IEEE Computer Graphics & Applications, Vol.11(5), pp.66-78, Sept.
1991.
Keywords :
Coding the shape of a solid or a surface in space amounts to representing it as a sequence of symbols. For manufactured solids, the shape is the result of a finite number of elementary operations, such that codings are available, either directly in the form of sequences of manufacturing commands or by using a few elementary shape primitives associated with these operations. In the case of natural objects such as those found in biology or medicine, a shape can have so many more degrees of freedom such that coding them demands some simplification, together with a loss of information and a gain in conceptualization. Topology is a mathematical means of performing such simplifications which, for instance, considers two objects as being equivalent if their points are given a one to one correspondence by a bicontinuous transformation. There are, however, many different topological classifications so that to choose one it is necessary to take into account such factors as the way data is obtained, or the purpose of the coding. This paper addresses objects determined from sections, with the experience of anatomical reconstructions from microscopic sections. The basic mathematical tool for interpreting the sections of 3-D objects is Morse theory, but we shall show that it is not sufficiently precise for our problem and we shall sketch some extensions to it.