|
|
July 13, 2000
BibTeX references.
P.J.Vermeer, PhD Thesis, 1994.
D. Dutta
& C.M. Hoffmann,
Journal of Mechanical Design, Vol. 115, pp.87-94, March 1993.
(1) Investigate geometric structures of Voronoi surfaces of simple CSG pairs. (2) Discuss trimming surfaces.
Simple CSG objects: Natural quadrics: block, sphere, cylinder and cone, as well as the torus.
Given 2 surfaces f and g, their Voronoi surface Vor(f,g) has 2 components:
Higher order symmetry: either part of a Voronoi curve or node.
Consider e.g. the interior skeleton of a rectangular block with a blind hole. In the vicinity of the bottom of the hole, the skeleton has 3 elements:
|
|
h2 demonstrate the need to consider Voronoi surfaces between surfaces and curves
Consider a Voronoi surface as the projection into (x,y,z) space of the intersection of two hypersurfaces in (x,y,z,r)-space. Each hypersurface is a generic r-offset. Two positive (negative) r-offsets intersect into an even Voronoi surface, while positive and negative offsets intersect into an odd Voronoi surface.
Let h = Vor(f,g), where f is a plane; then
| If g is a plane, then so is h. | |
| If g is a sphere, then h is a paraboloid of revolution. | |
| Let g be a cylinder. If the axis of g is parallel to or lies in f, then h is a parabolic cylinder. If the axis of g intersects f in a point, then h is a cone whose baseline corresponds to the elliptic or circular intersection of g and f. |
|
| If g is a cone, then so is h. If f contains the axis of g, then h has a hyperbola as base. If f does not contain the axis of g, nor its vertex, then h has the intersection of f and g as its base. |
|
| Let g be a torus. If f is perpendicular to the axis of the torus, then h is a quartic surface obtained by rotating a parabola about the axis. |
|
Let h = Vor(f,g), where f is a sphere; then
| If g is a sphere of equal radius, then h is a prolate spheroid (odd) or a plane (even). If g is a sphere of unequal radius, then h is a prolate spheroid (odd) or a two-sheeted hyperboloid (even). |
|
| If g is a cylinder whose axis contains the center of the sphere, then h is a plane or a surface obtained by rotating a parabola about a line perpendicular to the axis of symmetry. |
|
| If g is a cone whose axis contains the center of the sphere, then h is a figure of revolution, about the axis of the cone. The components of h are obtained by rotating a parabola around a line that is NOT perpendicular to the axis of symmetry. When g is tangent to f, then h has a component that is a right circular cone. |
|
| If g is a torus whose axis of revolution contains the center of the sphere, then h is a figure of revolution. Its components are obtained by revolving an ellipse or hyperbola around the torus axis. If the radius of g is equal to the minor radius of the torus, then h contains also a cone, a cylinder, or a plane. |
Let h = Vor(f,g), where f is a cylinder ; then
Let h = Vor(f,g), where f is a cone ; then
Let h = Vor(f,g), where f is a torus ; then
A suitable strategy for trimming away irrelevant surface areas must be devised that determines where the "influence region" of a face ends on an associated Voronoi surface. This is made difficult (numerically) by the fact that adjacent components of the skeleton can meet with tangent continuity.
Trimming of a Voronoi surface associated with f, should be done by a surface of normals at the boundary of f, i.e., a ruled surface generated by all the normals to f, along its boundary, e. N.B., this ruled surface is developable only if the associated boundary of f is along a line of (principal) curvature (hence not always the case). |
|
| Trimming surface at edge e. |
C.M.Hoffmann, 1991
The following 3 concepts fundamentally relate to measuring Euclidean distance, from a given geometric structure :
Considers compact objects (only) in E² and E³.
A specific difficulty is that the surfaces on which faces and edges of the 3D skeleton lie are not easily described using parametric or implicit algebraics that are commonly used by the geometric modeling community. In general, the surfaces can be described exactly and practically only using the dimensionality paradigm, as a system of nonlinear equations.
Cycles: Consider all oriented circles tangent at a point p of an oriented plane curve, C. With each such cycle, we associate a point q = (x, y, r), where (x, y) is the center of the cycle and r its radius (which is signed according to the orientation of the curve/cycle). For a given p the associated points q lie on line through p having a slope 1 against the (x,y)-plane. This line, when orthographically projected onto the (x,y)-plane, coincide with the normal of C through p.
Cyclographic map: Ruled surface, S(C), obtained, as p varies along C, by the lines defined by the sets of q's; these lines are called the generators of S. This map contains the distance surface of Blum. The points of S(C) which are not continuously differentiable are the skeleton w/r to C.
Direct recovery of the curve C from the MAT (see Fig.1) :
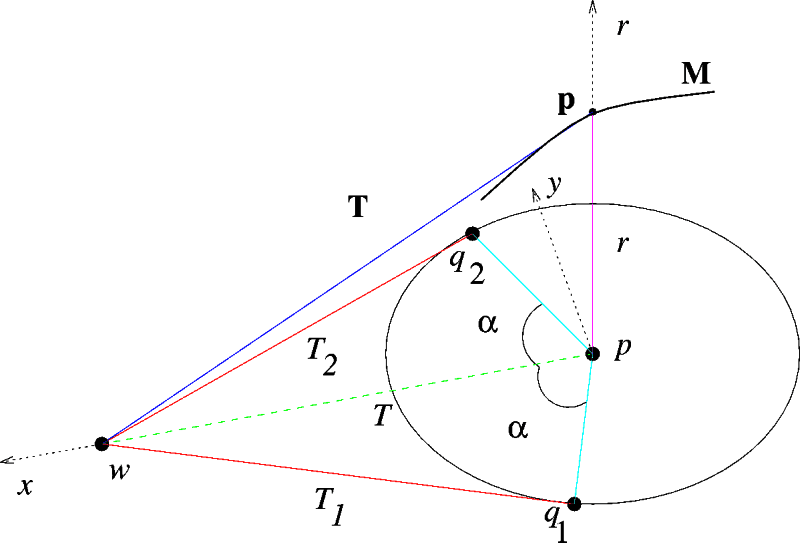
Figure 1 : Direct recovery of curve points (q1
& q2) from the MAT point P.
In 3D, the oriented circles are replaced by oriented spheres. For non-Euclidean metrics, one can choose suitable conics.
Consider a continuum of particles situated at time t = 0 on a plane, smooth curve C, moving at constant velocity in a direction locally normal to C. By the conservation of momentum, the kinetic energy of each particle is constant, and will be proportional to the squared velocity components in the principal directions. That is, Vx² + Vy² = 1, or
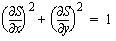 .
.
This is the Eikonal equation of geometrical optics (expressed in 2D Cartesian coordinates), where S(x,y) is the time when a particle reaches the point (x,y) (i.e., time of travel). Time can be taken for distance, and the Eikonal equation becomes a differential description of the Euclidean distance function. The 3D version (also expressed in Cartesian coordinates) is as follows:
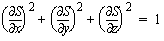 .
.
The Eikonal equation suggests integrating it to compute the Distance surface S, and extract MAT points by processing intersecting characteristics directions, during the integration.
C.M.Hoffmann and G. Vanecek, Jr., 1991
nD skeletons as the discontinuities of the graph of the distance map in (n+1)D space. Cyclographic map of Descriptive Geometry (generates the ruled & developable surface); its discontinuities form the skeleton. Relation with the Hamilton-Jacobi equation. The shocks of this PDE correspond to the skeleton.
Chiang, C-S., Hoffmann, C.M. and Lynch, R.E.
Technical Report CSD-TR-91-072,
Comp. Sci. Dept., Purdue U., 17 pages, October 1991.
Traditional techniques for computing offsets are local in nature and lack good criteria for eliminating possible self-intersections of the offset. Methods based on integrating differential equations or on image processing do not lack such criteria, but seem to require constructing the solution in the ambient space, i.e., in one dimension larger than the offset. We investigate such methods.
Keywords: medial axis transform, skeletons, Eikonal, Euclidean Distance Transforms,
Christof M. Hoffmann
Technical Report CSD-TR-1014,
CAPO Report CER-90-33
Comp. Sci. Dept., Purdue U., 17 pages, September 1990.
Also published in the:
Proceedings of the 4th IMA Conference " The Mathematics of
Surfaces", University of Bath, England
A. Bowyer & J. Davenport ed., Oxford University Press, pp.421-438,
1994
The main ideas:
The offset of a CSG is not necessarily a CSG object, since the tubular offset surfaces of certain edges are not natural quadrics. But, it is not necessary to construct the offset solid explicitly, for all proximity computations can be expressed in terms of the original boundary elements. Still, determining closest bisecting points between boundary elements requires considerably more machinery than solving two bivariate quadratic equations.
NB: Some of the closest bisecting "points" are curves or surfaces. The generalization of this algorithm to curved boundary elements will necessitate introducing techniques for solving general systems of algebraic equations. An approximation is possible however (for curved bounding elements): (i) sample the surface, (ii) construct the Voronoi diagram, (iii) eliminate certain Voronoi edges and surfaces.
Carrier of the boundary element: corresponding curve or surface of an edge or face (boundary elements).
Then the problem of finding nearest bisecting points of the boundary elements is reduced to finding the ones of the carriers, with footpoints on the boundary elements.
Consider a face F as a bounding element and its associated carrier, the surface f :
Finding nearest bisecting points between a pair of carriers f and g :
Solve the following system of algebraic equations:
Equations (1) and (2) assert that p is on f and q is on g. If f (or g) is a curve, then consider in lieu of equation (1) or (2) the intersection of two surfaces, f1 and f2: i.e., f1(p) = f2(p) = 0.
Equations (3) and (4) assert that the connecting line pq is normal to f at p, and to g at q, respectively.
The alebraic surfaces f and g are either a plane, a natural quadric (sphere, cone, cylinder) or a torus. It is helpful to consider a point to be a sphere of radius zero, a line to be a cylinder of radius zero and a circle to be a torus of minor radius zero.
Let g be a plane given by :
Most CSG surfaces f pose uninteresting problems, except the torus.
Theorem - Closest approach between a plane and a torus :
Let g be a sphere given by the vertex/center : q = (a, b, c)
Theorem - Closest approach to a point/sphere :
Let g be a cylinder given by its axis, as the parametric line:
Theorem - Closest approach to a line/cylinder :
Let g be a cone given by
Then the normals to this cone lie on cones with equation:
where l0 is the z-coordinate of the intersection of the normals with the cone axis.
Theorem - Closest approach to a cone :
Theorem - Closest approach between a pair of tori :
We represent the edges of CSG objects with carriers given as the intersection of 2 surfaces g and h, of degree 1, 2 or 4. The normal plane to the curve is spanned by the gradients to g and h, denoted Ng and Nh . The tangent vector to the curve is given by the cross product Ng x Nh .
The connection line pq between a point p on f and a point q on the curve g ^ h must lie in the normal plane to the curve at p. Let (x0, y0, z0) be a point on the curve where there is a linear combination of the surface normals that is perpendicular to f. For all cases this gives us 2 conditions:
Then additional conditions are found depending on the form of the surface f .
If f is a plane, say z = 0, then we have the 2 additional conditions:
If f is a sphere, e.g. with center q = (a,b,c), then we have the additional condition:
which states that a certain linear combination of the 2 normals is equal to the vector from the curve point to the center of the sphere. This is equivalent to 3 scalar equations.
The case of the cylinder, cone and torus are also treated.
The condition is now expressed as a point, p on a curve g1 ^ h1, which lie on the normal planes of the other point q on a curve g2 ^ h2, and vice-versa. Equivalently, the connection line is in both normal planes.
Amongst the computed nearest bisecting points, retain only those which are truly at minimum distance from their pair of bounding elements (and from no other bounding elements).
Each point of closest approach retained, p, will now have up to s (>= 2) boundary elements, Ei (i = 1, ... s). We can then build a list structure:
where r is the minimum distance of p from each boundary element Ei, and pi is a footpoint of p and Ei.
Each skeleton point p determined above is either on a face (s = 2), edge (s >= 3) or vertex (s >= 4) of the skeleton. The dimension of the tangent space at p of the r-offset intersection determines the topology of the skeleton in the neighborhood of p:
Of all the identified nearest bisecting points above, consider those which are part of skeleton edges (rank n-1) or vertices (rank n-2). We need now to determine their local topology, i.e., find their adjacent faces or edges, respectively.
The first section is located at ridges (l = 0) if the object surface contains locally convex edges.
It is then proposed to use a Distance Transform, i.e., the (x, y, z, r)-space, and look for possible intersection of faces or edges using a surface tracer like the marching-cube ... (this must not have been tested: no results provided in this or latter papers; might not work).
Sections are constructed by order of increasing distance (radius function).
D. Dutta
& C.M. Hoffmann,
Technical report, CSD-TR-955,
CAPO Report CER-90-10
Comp. Sci. Dept., Purdue U., 27 pages, February 1990.
Christoph Hoffmann and Jianhua Zhou
Technical report, CSD-TR-960,
Comp. Sci. Dept., Purdue U., 37 pages, May 1990.
Jung-Hong Chuang and Christoph Hoffmann
Technical report, CSD-TR-1015,
CAPO Report CER-90-34
Comp. Sci. Dept., Purdue U., 20 pages, September 1990.
Let F be a 2D manifold in n-D space, and let pi(F) be its projection int the subsapce of 3 of the variables in which F has been expressed. We give and algorithm that computes the normal curvature of pi(F) directly from the equations of F without variable elimination. We also comment on applications in CAGD.
Christoph Hoffmann
Technical report, CSD-TR-975,
Comp. Sci. Dept., Purdue U., 64 pages, April 1990.
We present methods for parameterizing implicit curves and surfaces and for implicitizing parametric curves and surfaces, based on computational techniques from algebraic geometry. After reviewing the basic mathematical facts or relevance, we describe and illustrate state-of-the-art algorithms and insights for the conversion problem.
Christoph Hoffmann
Technical report, CSD-TR-895,
Comp. Sci. Dept., Purdue U., 34 pages, July 1989.
Page created & maintained by Frederic Leymarie,
1998-2000.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu