Last update: April 6, 2007

BACK

Joachim Giesen et al.

• Critical Points of the Distance to an ε-Sampling on a Surface & Flow Based Surface Reconstruction, 2005.
• Shape Segmentation and Matching with Flow Discretization, 2003.
• Computing the Weighted Flow Complex, 2003.
• Alpha-Shapes and Flow Shapes are Homotopy Equivalent, 2003.
• The Flow Complex: A Data Structure for Geometric Modeling, 2003.
• Surface Reconstruction Based on a Dynamical System, 2002.
• The Complexity of Flow Diagrams in the Plane, 2002.
• Surface Reconstruction Using Umbrella Filters, 2002.
• New Techniques for Topologically Correct Surface Reconstruction, 2000.

Critical Points of the Distance to an ε-Sampling on a Surface and Flow Based Surface Reconstruction

Abstract

Summary

1. Introduction

• Every point p of S is closer to P than ε times lfs(p), where lfs(p) is the distance from p to the medial axis of S. Amenta and Bern proved that it is possible to extract from the Delaunay triangulation of P a piecewise linear surface that approximates S both topologically and geometrically.

2. Basic Concepts

• Minima : the sample points themselves
• Maxima: Voronoi vertices (A_1^4)
• Saddles: see below.
  

is a point, d(x), called the driver of the flow at x, and A(x) is the set of closest sample points (in P) to x

• Index 0: Stable manifold of an index-0 critical point: a local minimum (the sample p in P).
• Index 1: The index 1 critical point is a 1-saddle: intersection point of a Delaunay edge with its dual Voronoi facet. (NB(ffl): this is an A_1^2-2). The associated stable manifold is the Delaunay (Gabriel) edge.
  
• Index 2: The index 2 critical point is a 2-saddle (NB(ffl): an A_1^3-2). The associated stable manifold is a piecewise linear surface patch.
  
• Index 3: The index 3 critical point is a local maximum, a Voronoi vertex (NB(ffl): an A_1^4). 
  

• The dimension of each cell in the flow complex is the index of its associated critical point.
• Recursive structure: the boundary of the stable manifold of a critical point is made up of stable manifolds of critical points of lower indices.
  
• NB(ffl): This is the CW-Complex; e.g., see papers by J.C. Hart.
  

3. Separation of Critical Points

4. Algorithms

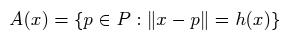
Web links:

• Ohio-State University/Dey
• WADS.org
• ToC
• Link @ Springer

Geometric shapes are identified with their features. For computational purposes a concrete mathematical definition of features is required. In this paper we use a topological approach, namely dynamical systems, to define features of shapes. To exploit this definition algorithmically we assume that a point sample of the shape is given as input from which features of the shape have to be approximated. We translate our definition of features to the discrete domain while mimicking the set-up developed for the continuous shapes. Experimental results show that our algorithms segment shapes in two and three dimensions into so-called features quite effectively. Further, we develop a shape matching algorithm that takes advantage of our robust feature segmentation step.

Web links:

• ACM portal

In this paper we establish a topological similarity between two apparently different shape constructors from a set of points. Shape constructors are geometric structures that transform finite point sets into continuous shapes. Due to their immense practical importance in geometric modeling various shape constructors have been proposed recently. Understanding the relations among them often leads to new insights that are potentially helpful in applications. Here we discover a topological equivalence among two such geometric structures, namely ? shapes and flow shapes. Both shapes found applications in surface reconstruction and molecular modeling.

Web links:

• ACM portal

Structuring finite sets of points is at the heart of computational geometry. Such point sets arise naturally in many applications. Examples in R³ are point sets sampled from the surface of a solid or the locations of atoms in a molecule. A first step in processing these point sets is to organize them in some data structure. Structuring a point set into a simplicial complex like the Delaunay triangulation has turned out to be appropriate for many modeling tasks. Here we introduce the flow complex which is another simplicial complex that can be computed efficiently from a finite set of points. The flow complex turned out to be well suited for surface reconstruction from a finite sample and for some tasks in structural biology. Here we study mathematical and algorithmic properties of the flow complex and show how to exploit it in applications.

Summary here.

We present an efficient algorithm that computes a manifold triangular mesh from a set of unorganized sample points in IR3. The algorithm builds on the observation made by several researchers that the Gabriel graph of the sample points provides a good surface description. However, this surface description is only one-dimensional. We associate the edges of the Gabriel graph with index 1 critical points of a dynamical system induced by the sample points. Exploiting also the information contained in the critical points of index 2 provides a two-dimensional surface description which can be easily turned into a manifold.

Web links:

• Conference site at the University of Lethbridge, Canada
• ToC

Earlier version as conference proceedings at Vis.'2000 (below).

We present a new approach to surface reconstruction in arbitrary dimensions based on the Delaunay complex. Basically, our algorithm picks locally a surface at each vertex. In the case of two dimensions we prove that this method gives indeed a reconstruction scheme. In three dimensions we show that for smooth regions of the surface this method works well and at difficult parts of the surface yields an output well-suited for postprocessing. As a postprocessing step we propose a topological clean up and a new technique based on linear programming in order to establish a topologically correct surface. These techniques should be useful also for many other reconstruction algorithms.

Author Keywords: Surface reconstruction; Gabriel graph; Linear programming

Subcomplexes of the Delaunay complex

A Delaunay simplex is s.t. that their exist an open ball empty of points of the finite set, S in R^d, other than the k (k <= d+1) points defining the ball (. The Delaunay complex (DC) is the collection of all such simplices.

The Alpha-shape (Edelsbrunner et al., 1994), is a sub-complex of the DC, s.t. each of its k-simplex corresponds to a maximal contact ball with radius alpha. For the purpose of surface reconstruction, consider only simplices of dimension k = d-1 (e.g., triangles in 3D).

The Beta-skeleton (Kirkpatrick & Radke, '1985) is a (d-1) complex defined by a forbidden zone as follows. Consider a (d-1) simplex sigma with d vertices. The simplex belongs to the Beta-skeleton, iff the union of the two d-dimensional balls tangent to the d vertices with diameter Beta * diam(sigma) is empty, where diam(sigma) is the smallest diameter of the balls.

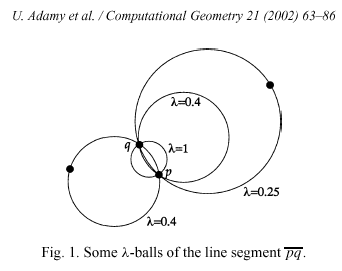
The Lambda-complex adapts to varying sampling density but is less restrictive than the Beta-skeleton. Let diam(sigma) be the diameter of the smallest circumscribed ball for a (d-1) simplex sigma. A Lambda-ball b_l(sigma) is an open d-dimensional ball with diameter diam(sigma)/l, l in (0,1], with all its vertices at its boundary. For l=0, b_l(sigma) is an open halfspace through the vertices of sigma.

NB: A Gabriel simplex is such that l = 1, i.e., it corresponds to the smallest circumscribed ball through d points. In 3D, it is the triangle of the maximal contact sphere through a triplet of points.

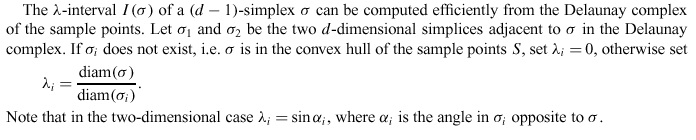
E.g., in 3D, consider a triangle as sigma. This triangle is the face of a pair of (Delaunay) tetrahedra, sigma_1 and sigma_2 (unless one of these recedes to infinity, i.e., sigma is a face of the convex hull of the set S).

NB: Consider the pair of A_1^4 shock nodes associated to the A_1^3 shock curve, dual to the triangle. They give directly the two diameters diam(sigma_i). Thus, this concept is similar to the idea (of Amenta et al.) of using "poles". That is, favor the triangles having associated longer shock curves (intituitively, longer or better defined "normals").

The Algorithm UmbrellaFilter

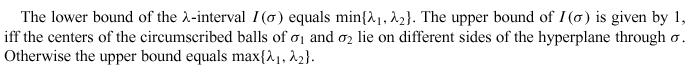
Lines 10-13 :

• Among all Gabriel simplices at a vertex v:
  • Successively choose the Gabriel simplex having minimal lower Lambda-interval bound
    i.e., having largest associated contact d-ball. E.g., if it is part of the convex hull, automatically pick it.
  • Proceed until an umbrella for v is obtained.
  • Discard remaining Gabriel simplices at v.

The Two-Dimensional Case

See text.

The Three-Dimensional Case

The umbrella check at a vertex v is done by constructing a graph G_v with vertex set V_v (the set of all vertices adjacent to v in the Gabriel complex). Each time a new triangle <v,v_1,v_2> is added to ChosenSimplices_v, the vertices v_1 and v_2 are connected by an edge in G_v. An umbrella at v is then a cycle in G_v.

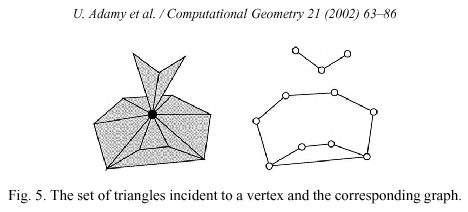
In practice, the above procedure does not always lead to a topologically correct surface.

NB: Condition (b) above does not permit to have a boundary for a surface (the assumption is one of a closed bounded surface).

Topological Clean Up

3 types of triangle sets which do not fulfill the "umbrella condition" (of existence, simplicity or uniqueness):

1. There are some triangles incident at v, but no closed cyle in G_v (no umbrella).
2. A triangle exist at v which is not part of an umbrella at v.
3. There is more than one umbrella through some triangle(s) incident at v.

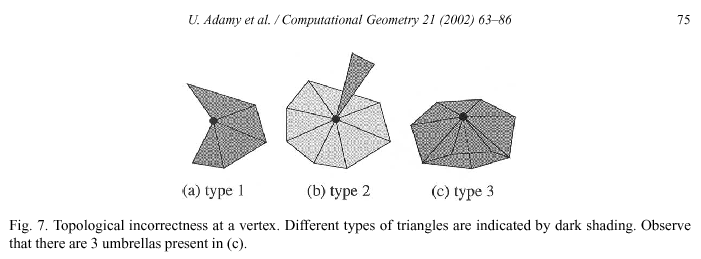
Delete type 2 triangles (direct).

Delete type 3 triangles in reverse order of the lower bounds of their Lambda-intervals (i.e., favor small lower Lambda-intervals). NB: this may make some remaining triangles of type 2.

A subset of vertices with type 1 triangles may correspond to [a] hole(s), H.

Establishing Closed Surfaces (closing holes)

NB: Earlier version of the journal paper (above).

We present a new approach to surface reconstruction based on the Delaunay complex. First we give a simple and fast algorithm that picks locally a surface at each vertex. For that, we introduce the concept of lambda-intervals. It turns out that for smooth regions of the surface this method works very well and at difficult parts of the surface yields an output well-suited for postprocessing. As a postprocessing step we propse a topological clean up and a new technique based on linear programming in order to establish a topologically correct surface. These techniques should be useful also for many other reconstruction schemes.

BACK

Page created & maintained by Frederic Leymarie, 2003-7.
Comments, suggestions, etc., mail to: ffl(at)gold(dot)ac(dot)uk