April 12, 2004

BACK

Publications in Computational Chemistry on Molecular Surfaces :

• Blaney, J. M. et al. :
  • Distance Geometry in Molecular Modeling, 1994.
• Boissonnat, J.-D. et al. :
  • Computing Connolly Surfaces, 1994
• Connolly, M.L. et al. :
  • Molecular Surfaces: Calculations, Uses and Representations, 2001.
  • Molecular Surfaces: A Review, 1996.
  • Molecular interstitial skeleton, 1991.
  • Shape distributions of protein topography, 1992.
• Gerstein, M & Richards, F.S. :
  • Protein Geometry: Distances, Areas, and Volumes, 2001
• Lin, S. L. et al. :
  • Molecular surface representations by sparse critical points, 1994.
• Sanner, Michel F. et al. :
  • Modelling and Applications of Molecular Surfaces, PhD, 1992.
• Will, Hans-Martin :
  • Fast and efficient computation of additively weighted Voronoi cells for applications in molecular biology, 1998.

BibTeX references.

Web site: http://bioinfo.mbb.yale.edu/geometry/

1. Introduction
2. Geometric Definitions
   1. Definitions of Volume
      1. The Voronoi Construction
      2. The Delaunay Triangulation
   2. The Problem of the Protein Surface\
   3. Definitions of Surface
   4. Definitions of Atomic Radii
      1. van der Waals radii
      2. Probe radius
3. Applications and Results
   1. Packing
      1. Using Volume to Measure Packing Efficiency
      2. How tightly packed is the protein core?
      3. Surface Packing
      4. Internal Interfaces and Motions
   2. Cavities

Figure #1 - 2D schematic of the Voronoi Construction

Figure #2 - A Voronoi Polyhedron in 3D

Figure #3 - The Positioning of the Dividing Plane

Figure #4 - The Delaunay Triangulation

Figure #5 - Open Polyhedra on the Protein Surface

Figure #6 - Various Definitions of Protein Area

Figure #7 - Packing Efficiency

Figure #8 - Tight Packing vs. Loose Packing

Table #1 - Lists of vdW radii

Table #2 - Some Surfaces

Table #4 - Standard Volumes for Atoms in the Core

PDF (per section) files.

Key-words: Computational geometry, Voronoï diagrams, Delaunay diagrams, Pavings, Molecular modeling, Molecular cavities, Connolly surface, Surface fitting.

Molecular modeling of biological molecules aims to elucidate mechanisms at the molecular level and enable the design of drugs with a specific action. We propose new solutions to some problems related to the simulation of molecular interactions. In the first part, we undertake a mathematical study of the Lee-Richards and the Connolly surfaces [Co 83]. We prove that this last surface is made of spheric contact faces, spheric reentrant faces and torique reentrant faces. In the second part, we present the concept of maps and its extension to the three dimensional space using the concept of pavings first introduced by J.C. Spehner [Sp 91]. These data structures are subsequently used in the developed algorithms. In the third part, we define the Voronoï and the Delaunay diagrams for a set S, of sites. We prove some properties of these diagrams, and show their usefulness in molecular modeling. We study the size of Delaunay diagrams when the sites of S are the center of atoms of a biological molecule. In this case, we observed that both the number of Delaunay regions and the number of Delaunay faces behave as linear functions of the number of sites. We present an algorithm to compute a set of tetrahedra inscribed in the Delaunay spheres. An optimal algorithm, given by M. Elbaz and J.C. Spehner [El 92], to compute the Delaunay diagram is also given. We show that under some assumptions on the spheres centered in S, the complexity of this algorithms are respectively in O(n2) and in O(nlogn). These assumptions are fulfilled when the set of spheres represents a molecule. In the fourth part, we present a model of molecular cavities, consisting of a set of spheres obtained by reduction of the Delaunay spheres. We define locally maximal spheres and prove that all these spheres belong to our model. The spheres of the model are connected by tunnels. The radius of such a tunnel corresponds to the size of the largest sphere that can pass from one Delaunay sphere to the next without intersecting any atom. The model is obtained by sculpting the convex hull of the Delaunay diagram. This algorithm presents some similarities with the sculpture algorithm introduced by J.D. Boissonnat [Bo 84]. A characteristic of our method is its ability to distinguish between internal and open cavities. Its complexity is a linear function of the number of faces in the Delaunay diagram. The fifth part is dedicated to the study of the Delaunay separation space of two sets of spheres and its applications to molecular modeling. We define the notion of surrounding set of spheres and we present an algorithm, based on this notion, to compute a molecular surface approximating to the Connolly surface. We define the separation surfaces of two set of spheres. These surfaces are then used to evaluate the area of the surfaces in contact when two molecules interact. This method is able to differentiate between the contact surface and the buried surface. In the last part, we define the reduced surface of a set of spheres and prove a duality to the Lee-Richards surface. We present an algorithm to compute the reduced surface starting from the hull obtained after the sculpture of the Delaunay diagram presented in the fourth part. The complexity of this algorithm is in O(n2) where n is the number of spheres, but we show that under some assumptions about the set of spheres, there is an algorithm to compute the reduced surface in a time in O(nlogn). The set of spheres representing a biological molecule fulfills these conditions. We show that the reduced surface allows a set of polygons, approximating to the Connolly surface, to be built. An algorithm to refine this surface description to any level of detail is also described.

References

[Bo 84] J.D. Boissonnat. Geometric Structures for Three-Dimensional Shape Representation. ACM Transaction on Graphics, Vol 3, No 4, 266-286, October, (1984).

[Co 83] M.L. Connolly. Solvent Accessible Surfaces of Proteins and Nucleic Acids, Science, (1983), 221, No 4612.

[El 92] M. Elbaz. Sur les diagrammes de Voronoï et de Delaunay dans le plan et dans l'espace. Thèse Université de Haute-Alsace, (1992).

[Sp 91] J.C. Spehner. Merging in maps and pavings. Theoret. Comput. Sci. 86, (1991), 205-232.

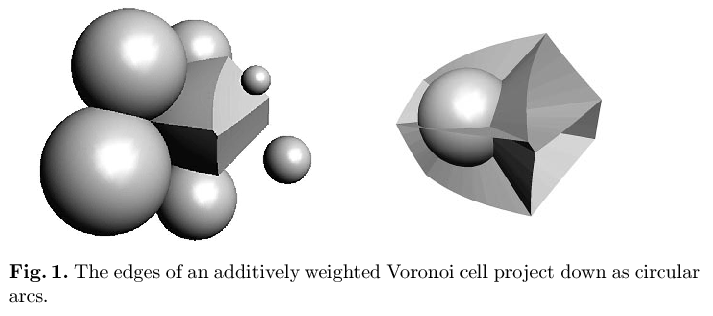
This paper is concerned with the efficient computation of additively weighted Voronoi cells for applications in molecular biology. We propose a projection map for the representation of these cells leading to a surprising insight into their geometry. We present a randomized algorithm computing one such cell amidst n other spheres in expected time O(n² log n). Since the best known upper bound on the complexity such a cell is O(n²), this is optimal up to a logarithmic factor. However, the experimentally observed behavior of the complexity of these cells is linear in n. In this case our algorith performs the task in expected time O(n log² n). A variant of this algorithm was implemented and performs well on problem instances from molecular biology.

BACK

Page created & maintained by Frederic Leymarie, 2000-4.
Comments, suggestions, etc., mail to: leymarie@lems.brown.edu